|
Biorithm
1.1
|
|
Biorithm
1.1
|
This program implements several algorithms for performing functional enrichment. For this type of analysis, the user typically possesses a set of "interesting" genes, e.g., a collection of genes that are significantly differentially expressed between treatment and control samples. Now, given a collection of curated gene sets (e.g., annotations from the Gene Ontology), we can evaluate the functional coherence of the "interesting" genes by analyzing their relationship or overlap to each of the curated gene sets (or collections of curated gene sets) and by measuring the statistical significance of the overlap. Ultimately, each of these functional enrichment algorithms returns a list of the curated gene sets that relate closely to the interesting set of genes. Such analysis provides a high-level summary of the interesting genes.
Download the Biorithm package and follow the installation instructions for Biorithm. The b>enrich executable will be available in the enrich subdirectory of Biorithm.
enrich includes several published functional enrichment algorithms: Fisher's exact test, GenGO [6], Parametric Analysis of Gene Set Enrichment (PAGE) [4], FuncAssociate [1], and two variations of Network-Based Enrichment [14], which we developed. Below, we describe the general command for invoking the available enrichment algorithms through enrich. Since Fisher's Exact Test is perhaps the most well-known enrichment method, we describe this algorithm in detail, with examples of how it can be executed using the enrich tool. Additionally, we elaborate on the two flavors of Network-Based Enrichment (NBE), as these algorithms were developed by our research group. For details regarding the other enrichment algorithms, please visit their respective publications linked above.
enrich accepts four different categories of command line options. See the table below for details about all available command line options. We briefly describe each category of options:
Exactly one of these options is required to specify which enrichment algorithm to run. enrich will print an error to standard output if the user provides an incorrect number of algorithms.
The user must use exactly one of these options to specify the universal collection of genes (e.g., all genes tested in a treatment-control microarray contrast). The universal collection of genes can be provided as simply a set of genes (-S), a network (-N), or a ranked list of genes (-R). Note that some algorithms require providing the universe through a specific option. For example, network-based enrichment clearly requires a network; if the universe is not provided using the required option, enrich will issue an error message to the standard output. Many algorithms only require the set of universal genes (e.g., GenGO). In this case, if the universe is provided as a network or ranked list, enrich internally converts these to the appropriate set of genes defined by the nodes in the network or the ranked list, respectively.
Exactly one of these options is required to specify the collection of "interesting" genes on which the user wants to perform functional enrichment (e.g., the most differentially expressed genes from a treatment-control contrast). This collection of genes should be a subset of the "Universe" set of genes. The "interesting" cluster of genes can be provided as simply a set of genes (-s), a network (-n), or a ranked list of genes (-r). Note that some algorithms require providing the cluster in a specific format. For example, network-based enrichment clearly requires a network; if the cluster is not provided using the required option, enrich will issue an error message to the standard output. Many algorithms only require the set of genes in the cluster (e.g., GenGO). In this case, if the cluster is provided as a network or ranked list, enrich internally converts these to the appropriate set of genes defined by the nodes in the network or the ranked list, respectively. There is a fourth option (-d) used for algorithms that do not require any cluster. Currently, PAGE is the only algorithm to which this option applies.
These options control various parametric aspects of running the enrichment algorithms. Of these, the --annotations-file (-a) is required to specify the curated gene sets (functional annotations). Many of the other options pertain only to certain enrichment algorithms, and these have reasonable default values. Please refer to the table below for detailed descriptions of these options.
In summary, a typical invocation of any enrichment algorithm will look like the following command (here, a set of flags inside square brackets indicates that the user should provide only one of the flags on the command line):
enrich <algorithm> -[NSR] <universe> -[nsrd] <cluster> -a <annotations> -o <output>
The detailed list of options supported by enrich are given in the following table.
| Flag | Long | Description | |
|---|---|---|---|
| ENRICHMENT ALGORITHMS | - | funcassociate | Run the FuncAssociate algorithm. |
| - | gengo | Run the GenGO algorithm. The user should provide the '--gengo-p' and '--gengo-q' options along with this option since we have not implemented the extension to GenGO that can learn these parameters. By default, p and q take the values suggested in the GenGO publication. | |
| - | hypergeometric | Perform the hypergeometric enrichment, i.e., Fisher's exact, test. | |
| - | page | Run the Parametric Analysis of Gene Set Enrichment (PAGE) algorithm Note that no cluster is provided with this algorithm, so you must use the --cluster-dummy option. | |
| - | random-function | Perform network-based enrichment, using the random function algorithm.
| |
| - | random-universe | Perform network-based enrichment, using the random universe algorithm.
| |
| UNIVERSE | N | universe-network | The name of the tab-delimited file containing the universal molecular interaction network. Each line represents a single edge in the network and may have 2-4 columns. The first two columns of each line must contain the identifiers of a pair of nodes connected by an edge. An optional third column can specify a type for the edge. An optional fourth column contains the weight of the edge. |
| S | universe-set | The name of the file containing the universal set of genes. Each line contains one gene name. | |
| R | universe-ranked-list | The name of a file containing a ranked universe of genes. The first line should contain header items; each subsequent line contains two tab-delimited items: identifier, value. | |
| CLUSTER | n | cluster-network | The name of the tab-delimited file containing the cluster as an interaction network. Each line represents a single edge in the network and may have 2-4 columns. The first two columns of each line must contain the identifiers of a pair of nodes connected by an edge. An optional third column can specify a type for the edge. An optional fourth column contains the weight of the edge. |
| s | cluster-set | The name of the file containing the cluster set of genes. Each line contains one identifier. | |
| r | cluster-ranked-list | The name of a file containing a ranked cluster of genes. The first line should contain header items; each subsequent line contains two tab-delimited items: identifier, value. | |
| d | cluster-dummy | Use this option with no argument for algorithms that do not require a cluster (e.g., PAGE). | |
| ENRICHMENT OPTIONS | o | output | The name of the file in which to write the results. |
| - | rand-seed | An integer used to seed the C++ rand() function. | |
| - | annotations-category | The category of annotations on which to perform functional enrichment (e.g., 'p', 'f', or 'c' for biological process, molecular function, or cellular component when working with GO annotations). When left blank, all categories will be used. | |
| a | annotations-file | Name of file containing a list of genes and their functional annotations or other attributes. The first line of the file contains the column names. Each tab-delimited line contains the gene id in column 'orf', the function id in column 'goid', the function category in column 'hierarchy', the evidence code in column 'evidencecode', and the annotation status 1, 0, or -1, in column 'annotation type'. If these are GO annotations, the program will transfer functional annotations up the GO DAG in accordance with the true path rule. | |
| - | functions-restriction-file | Name of a file containing a list of gene functions. Enrichment will be restricted to only functions listed in this file that also appear in the annotations given with the -a option. | |
| - | gengo-p | The probability value p for the GenGO algorithm. | |
| - | gengo-q | The probability value q for the GenGO algorithm. | |
| - | gengo-penalty | The penalty value for the inclusion of a function in the GenGO algorithm. | |
| - | num-edge-swap-iterations | For enrichment algorithms that require random graphs using the edge-swap graph randomization technique, this number specifies how many iterations to run the graph randomization algorithm. Note that the given integer k specifies that k*|E| iterations will be run. | |
| - | num-random-graphs | For enrichment algorithms that require graph randomization, this number specifies how many random graphs to generate. | |
| g | go-obo-file | The name of a file containing the definition of the Gene Ontology in OBO format. | |
| u | universe-type | Describes how the universe of genes should be determined for enrichment methods. 'all' denotes that all genes in the given universe network (or gene set) will define the true universe. 'intersection' denotes that the intersection of annotated genes and genes in the universe network (or gene set) will define the true universe. |
A standard formulation of the problem of functional enrichment is the following. We are given:
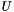
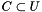
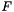 , where for each function
, where for each function 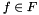 ,
, 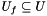 denotes the set of universal genes annotated by
denotes the set of universal genes annotated by 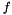 .
. We are interested in assessing the functional coherence of 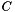 based on the annotation of its genes, given by
based on the annotation of its genes, given by 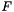 . Fisher's exact test addresses this problem for each function by answering the following question: "If we select a set
. Fisher's exact test addresses this problem for each function by answering the following question: "If we select a set 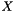 of
of 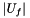 genes uniformly at random (without replacement) from the set of all genes
genes uniformly at random (without replacement) from the set of all genes 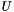 , what is the probability that the
, what is the probability that the 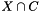 will contain
will contain 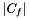 or more genes?", where
or more genes?", where 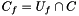 . It is well-known that this probability can be determined by computing the tail of the hypergeometric distribution as follows:
. It is well-known that this probability can be determined by computing the tail of the hypergeometric distribution as follows:
![\[ p_{fisher}(|U|, |C|, |U_f|, |C_f|) = \sum_{i=|C_f|}^{\min(|C|, |U_f|)} \frac{{|C| \choose i} {|U|-|C| \choose |U_f|-i}}{{|U| \choose |U_f|}}. \]](form_12.png)
enrich can be used to calculate this score for each function using the following command:
enrich --hypergeometric -S <universe-set> -s <cluster-set> -a <annotations> -o hyp-results.tsv
The resulting output file will contain one row for each function tested for enrichment, and several columns of information are printed for each row:
| Column Header | Description |
|---|---|
| algorithm | The enrichment algorithm used; in this case, 'hypergeometric' |
| func_id | An identifier for the function provided in the annotations file |
| func_category | The category of the function |
| universe_size | The number of genes in the universal set of genes |
| cluster_size | The number of genes in the interesting collection of genes |
| V_f | The number of genes in the universe that are annotated with the function |
| C_f | The number of genes in the cluster that are annotated with the function |
| hyp_pvalue | The hypergeometric p-value calculated using the four values from the previous four columns |
We developed two network-based functional enrichment algorithms that take into account an underlying network of interactions among the genes being analyzed. These two methods can be accessed through the enrich tool using the --random-function or --random-universe options as the algorithm when invoking enrich. Since the two NBE algorithms operate on networks, they require that the universe and cluster are provided using the -N and -n options, respectively. Details and applications of the Random Function and Random Universe NBE methods to biological datasets are available in the publication. We briefly describe the differences between these algorithms below.
The random function NBE approach for computing the statistical significance of each function strongly parallels the sampling-based alternative to the analytical solution for the one-sided version of Fisher's Exact Test. In the sampling-based solution for Fisher's exact test we repeatedly select a set 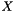 of size
of size 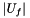 uniformly at random from the universe of genes
uniformly at random from the universe of genes 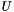 . We then calculate an empirical p-value for the function
. We then calculate an empirical p-value for the function 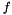 , which represents the statistical siginificance of the size of
, which represents the statistical siginificance of the size of 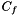 , as the fraction of samples for which the size of the intersection between the randomly selected set
, as the fraction of samples for which the size of the intersection between the randomly selected set 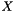 and the interesting collection of genes is at least as large as
and the interesting collection of genes is at least as large as 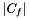 . If we repeat this process many times, the empirical value converges to the analytical solution (
. If we repeat this process many times, the empirical value converges to the analytical solution ( 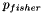 ). For the random function NBE method, rather than analyzing the statistical significance of the size of
). For the random function NBE method, rather than analyzing the statistical significance of the size of 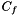 , we assess the statstical significance of the connectivity among the genes in
, we assess the statstical significance of the connectivity among the genes in 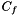 .
.
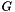 (given by the
(given by the -N option). We repeatedly generate a randomized universal network, 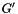 , with the same degree sequence as
, with the same degree sequence as 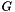 , i.e., the degree of each node is the same in
, i.e., the degree of each node is the same in 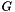 and in each randomized network
and in each randomized network 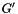 . The randomization procedure preserves topological properties of molecular interaction networks, such as their scale-free degree distribution. The
. The randomization procedure preserves topological properties of molecular interaction networks, such as their scale-free degree distribution. The --num-edge-swap-iterations controls how long the underlying graph randomization algorithm should run before using the randomized network. We assess the significance of each function based on the fraction of random networks ( 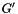 ) for which the connectivity among the genes in
) for which the connectivity among the genes in 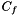 improved, compared to their original connectivity in the universal network (
improved, compared to their original connectivity in the universal network ( 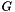 ).
). Both algorithms utilize sampling-based procedures to estimate a p-value representing the statistical significance of each function. Thus, these algorithms may be quite time-consuming depending on the number of functions tested and the number of sampling iterations used. The number of sampling iterations can be controlled for either method using the --num-random-graphs option.
The following sample command demonstrates how to execute the random universe NBE algorithm for 1000 random networks (i.e., minimum p-value of 0.001):
enrich --random-universe -N <universal-network> -n <cluster-network> -a <annotations> --num-random-graphs 1000 -o nbe-results.tsv
The resulting output file will contain one row for each function tested for enrichment, and several columns of information in each row. The same columns as those reported for the Fisher's Exact Test are included in the NBE output files. Additionally, several network statistics about 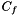 are provided. Perhaps the most relevent of the network statistics columns is the one with the header "lex_components_by_nodes_pvalue". This column contains the p-values that are discussed in the publication of these NBE methods.
are provided. Perhaps the most relevent of the network statistics columns is the one with the header "lex_components_by_nodes_pvalue". This column contains the p-values that are discussed in the publication of these NBE methods.
 1.7.6.1
1.7.6.1