|
Biorithm
1.1
|
|
Biorithm
1.1
|
The reconcile tool implements several methods that reconcile gene expression data with an underlying molecular interaction network. For this type of analysis, the user typically possesses a (possibly weighted) undirected interaction network and weights for some or all of the nodes in the network. Higher weight indicates greater importance for that node. For example, given treatment and control gene expression samples, we could use limma to compute a p-value representing the statistical significance of the level of differential expression of the gene between treatment and control. By taking the negative logarithm of each gene's p-value, we have an initial score for each gene where high scores represent a large degree of differential expression. The reconciliation algorithms weight each node in the underlying interaction network by these initial node scores and proceed to diffuse this value throughout the network. The diffusion process typically ensures that scores on neighboring nodes are similar, while each node's score does not deviate too much from its initial weight.
Download the Biorithm package and follow the installation instructions for Biorithm. The reconcile executable will be available in the reconcile subdirectory of Biorithm.
reconcile accepts three different categories of command line options:
Exactly one of these options specifies which reconciliation algorithm to run. reconcile will print an error to standard output if the user provides an incorrect number of algorithms.
| Flag | Long | Description |
|---|---|---|
| - | vanilla | Compute node scores by minimizing the energy function for the Vanilla algorithm. |
| - | pagerank | Compute node scores by minimizing the energy function for the PageRank algorithm. |
| - | genemania | Compute node scores by minimizing the energy function for the GeneMANIA algorithm. |
| - | heat-kernel | Compute node scores by applying the heat diffusion kernel. |
Each algorithm can be run in two different ways. The user can provide multiple networks (-N) and the chosen algorithm will be run on each network using uniform start weights for each node. Alternatively, the user can provide a single network (-n) and one or more collections of node weights (-W), and the chosen algorithm will be run on the same network using the various specified starting node weights.
| Flag | Long | Description |
|---|---|---|
| N | networks | Name of the tab-delimited file containing multiple interaction networks with the following 5-column format: graphId, node1, node2, edge type, edge weight. The last 2 columns are optional. |
| W | node-weights | Name of the tab-delimited file containing node weights. The first column contains node identifiers, and remaining columns contains node weights, each column for a different sample. |
| n | network-file | Name of the tab-delimited file containing the interaction network with the following 2-column format: node1, node2. An optional 3rd column may be provided with edge-weight. Other columns will be ignored. |
These options control various parametric aspects of running the network reconciliation algorithms.
| Flag | Long | Description |
|---|---|---|
| - | max-num-iterations | An integer that controls the maximum number of iterations for the reconciliation algorithms before terminating. |
| - | epsilon | A small value used for checking convergence of reconciliation algorithms. |
| q | q-param | The parameter 0<q<=1 in some reconciliation algorithms. In the case of the HeatKernel method, the temperature is given by 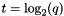 . High q gives more weight to the initial node values, while low q gives more weight to the network-based term in the energy function. . High q gives more weight to the initial node values, while low q gives more weight to the network-based term in the energy function. |
| o | output | A prefix for the output files that are generated by the reconciliation algorithms. |
A typical invocation of any network reconciliation algorithm will look like the following command:
reconcile --<algorithm> -n <network> -W <node-weights> -o <output>
If the -N option is used, an output file is generated for each input network. If the -n and -W options are used, an output file is generated for each sample in the input weights matrix. Each output file contains one row for each node in the network and several columns of information for the node in each row:
| Column Header | Description |
|---|---|
| NodeId | The node identifier. |
| initial_<sample-name> | The initial node value for the current sample. Sample name is determined by the column header of that sample in the weights file. |
| final_<sample-name> | The final node value for the current sample. |
| degree | The number of neighbors for this node in the network. |
| weighted_deg | The sum of the weights of the edges incident on this node in the network. |
Let 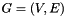 be an undirected network, where
be an undirected network, where 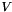 is the set of nodes and
is the set of nodes and 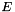 is the set of edges. Denote the weight of edge
is the set of edges. Denote the weight of edge 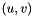 by
by 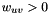 . Let
. Let 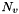 denote the neighbors of node
denote the neighbors of node 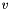 in the graph, and let
in the graph, and let 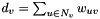 denote the weighted degree of node
denote the weighted degree of node 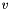 . Let
. Let 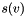 be the starting value of node
be the starting value of node 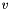 (specified by the
(specified by the -W option). Each network reconciliation algorithm computes a final score 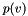 for each node
for each node 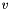 by smoothing the initial node scores across the network.
by smoothing the initial node scores across the network.
![\[ \mathcal{E} = q \sum_{v \in V} \big( p(v)-s(v) \big)^2 + (1-q) \sum_{(u, v) \in E} w_{uv} \big( p(v)-p(u) \big)^2 \]](form_36.png)
 is a quadratic function of the
is a quadratic function of the 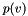 values, we can minimize it by setting its partial derivative with respect to each
values, we can minimize it by setting its partial derivative with respect to each 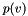 to 0, resulting in the following linear system:
to 0, resulting in the following linear system:
![\[ p(v) = \frac{qs(v) + (1-q)\sum_{u\in N_v} w_{uv}p(u)}{q+(1-q)d_v} \]](form_38.png)
![\[ \mathcal{E} = q \sum_{v \in V} \frac{\left( p(v)-s(v) \right)^2}{d_v} + (1-q) \sum_{(u, v) \in E} w_{uv} \left( \frac{p(v)}{d_v}-\frac{p(u)}{d_u} \right)^2 \]](form_39.png)
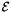 is a quadratic function of the
is a quadratic function of the 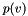 values, we can minimize it by setting its partial derivative with respect to each
values, we can minimize it by setting its partial derivative with respect to each 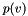 to 0, resulting in the following linear system:
to 0, resulting in the following linear system:
![\[ p(v) = qs(v) + (1-q)\sum_{u\in N_v} \frac{w_{uv}}{d_v}p(u) \]](form_40.png)
![\[ \mathcal{E} = q \sum_{v \in V} \left( p(v)-s(v) \right)^2 + (1-q) \sum_{(u, v) \in E} w_{uv} \left( \frac{p(v)}{\sqrt{d_v}}-\frac{p(u)}{\sqrt{d_u}} \right)^2 \]](form_41.png)
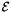 is a quadratic function of the
is a quadratic function of the 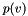 values, we can minimize it by setting its partial derivative with respect to each
values, we can minimize it by setting its partial derivative with respect to each 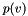 to 0, resulting in the following linear system:
to 0, resulting in the following linear system:
![\[ p(v) = qs(v) + (1-q)\sum_{u\in N_v} \frac{ w_{uv} }{ \sqrt{d_ud_v} }p(u) \]](form_42.png)
![\[ \mathbf{p} = \sum_k=0^\infty \frac{(-t)^k}{k!}L^k\mathbf{s} = e^{-tL}\mathbf{s} \]](form_43.png)
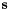 and
and 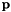 are the vectors of starting and final values, repsectively, and
are the vectors of starting and final values, repsectively, and 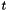 parameterizes the rate of heat dispersion through the network. We define
parameterizes the rate of heat dispersion through the network. We define 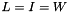 , where
, where 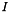 is the identity matrix, and
is the identity matrix, and 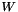 is a normalized edge weith matrix such that
is a normalized edge weith matrix such that 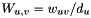 . We use the following approximation for the above matrix exponential:
. We use the following approximation for the above matrix exponential:
![\[ \mathbf{p} = \left(I-\frac{t}{n}L\right)^n\mathbf{s} \]](form_51.png)
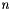 tends to infinity. Let
tends to infinity. Let 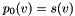 and recursively define
and recursively define 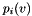 as follows:
as follows:
![\[ p_i(v) = p_{i-1}(v) + \frac{t}{n}\sum_u L_{u,v} P_{i-1}(u) = \left( 1-\frac{t}{n} \right) p_{i-1}(v) + \frac{t}{n}\sum_{u \in N_v} W_{u,v} p_{i-1}(u) \]](form_54.png)
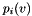 up to
up to 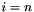 , where
, where 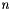 is supplied by the user (
is supplied by the user (--max-num-iterations).  1.7.6.1
1.7.6.1